




Next: Dijkstra(flexible) ( GIT_DIJKSTRA )
Up: Graphs and Iterators
Previous: Topological Sort (flexible) (
Contents
Index
Strongly Connected Components (flexible) ( GIT_SCC )
Definition
An instance algorithm of class GIT_SCC< Out, In, It, OutSt, InSt, NSt, Mark > is
an implementation of an algorithm that computes
the strongly connected components.
Iterator version: There is an iterator version of this algorithm:
SCC_It. Usage is similar to that of node iterators without
the ability to go backward in the sequence and only a graph is
allowed at creation time. Method compnumb() returns the component
number of the current node.
#include < LEDA/graph/graph_iterator.h >
Creation
| GIT_SCC< Out, In, It, OutSt, InSt, NSt, Mark > |
algorithm(OutSt ost, InSt ist, Mark ma, Out oai, const It& it, In iai) |
| |
|
creates an instance algorithm of this class bound to
the stack st and data accessor ma.
|
Preconditions:
- Out is an adjacency iterator that iterates over the
outgoing edges of a fixed vertex
- In is an adjacency iterator that iterates over the
incoming edges of a fixed vertex
- OutSt is stack parameterized with items of type Out
- InSt is stack parameterized with items of type In
- Mark is a data accessor that has access to a boolean value
that is associated with each node of the graph
Operations
| int |
algorithm.state() |
returns the internal state.
|
- NEXT_OUT =first phase,
- NEXT_ORDER =order phase,
- NEXT_IN=second phase,
- NEXT_DONE =algorithm finished
| void |
algorithm.finish_algo() |
executes the algorithm until finished() is true.
|
| bool |
algorithm.finished() |
returns true if the algorithm is finished.
|
| InSt& |
algorithm.get_in_stack() |
gives direct access to the internal stack of incoming adjacency iterators.
|
| In |
algorithm.in_current() |
returns the current iterator of the internal stack of incoming
adjacency iterators.
|
| OutSt& |
algorithm.get_out_stack() |
gives direct access to the internal stack of outgoing adjacency iterators.
|
| Out |
algorithm.out_current() |
returns the current iterator of the internal stack of outgoing
adjacency iterators.
|
| itnodetype |
algorithm.current_node() |
returns the current node.
|
| int |
algorithm.compnumb() |
returns the component number of the fixed node of the current
iterator if current state is NEXT_IN.
|
| int |
algorithm.next() |
Performs one iteration of the core loop of the algorithm.
|
Implementation
Each operation requires constant time.
The algorithm has running time
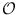 (| V| + | E|).
(| V| + | E|).





Next: Dijkstra(flexible) ( GIT_DIJKSTRA )
Up: Graphs and Iterators
Previous: Topological Sort (flexible) (
Contents
Index





![]() (| V| + | E|).
(| V| + | E|).




