| vector |
v |
creates an instance v of type vector; v is initialized to
the zero-dimensional vector.
|
| vector |
v(int d) |
creates an instance v of type vector; v is initialized to
the zero vector of dimension d.
|
| vector |
v(double a, double b) |
creates an instance v of type vector; v is initialized to
the two-dimensional vector (a, b).
|
| vector |
v(double a, double b, double c) |
| |
|
creates an instance v of type vector; v is initialized to
the three-dimensional vector (a, b, c).
|
| vector |
v(const vector& w, int prec) |
| |
|
creates an instance v of type vector; v is initialized to
a copy of w. The second argument is for
compatibility with rat_vector.
|
| int |
v.dim() |
returns the dimension of v.
|
| double& |
v[int i] |
returns i-th component of v.
Precondition
0 < = i < = v.dim()-1.
|
| double |
v.hcoord(int i) |
for compatibility with rat_vector.
|
| double |
v.coord(int i) |
for compatibility with rat_vector.
|
| double |
v.sqr_length() |
returns the square of the Euclidean length of v.
|
| double |
v.length() |
returns the Euclidean length of v.
|
| vector |
v.norm() |
returns v normalized.
|
| double |
v.angle(const vector& w) |
returns the angle between v and w.
|
| vector |
v.rotate90(int i=1) |
returns v by an angle of
i x 90 degrees.
If i > 0 the rotation is counter-clockwise otherwise
it is clockwise. Precondition
v.dim() = 2
|
| vector |
v.rotate(double a) |
returns the v rotated counter-clockwise by an angle of a (in radian).
Precondition
v.dim() = 2
|
| vector& |
v += const vector& v1 |
Addition and assign.
Precondition v.dim() = v1.dim().
|
| vector& |
v -= const vector& v1 |
Subtraction and assign.
Precondition v.dim() = v1.dim().
|
| vector |
v + const vector& v1 |
Addition.
Precondition v.dim() = v1.dim().
|
| vector |
v - const vector& v1 |
Subtraction.
Precondition v.dim() = v1.dim().
|
| double |
v * const vector& v1 |
Scalar multiplication.
Precondition v.dim() = v1.dim().
|
| vector |
v * double r |
Componentwise multiplication with double r.
|
| vector& |
v *= double r |
multiplies all coordinates by r.
|
| vector |
v / double r |
Componentwise division which double r.
|
| bool |
v == const vector& w |
Test for equality.
|
| bool |
v != const vector& w |
Test for inequality.
|
| void |
v.print(ostream& O) |
prints v componentwise to ostream O.
|
| void |
v.print() |
prints v to cout.
|
| void |
v.read(istream& I) |
reads
d = v.dim() numbers from input stream I and writes
them into
v[0]...v[d - 1].
|
| void |
v.read() |
reads v from cin.
|
| ostream& |
ostream& O « const vector& v |
| |
|
writes v componentwise to the output stream O.
|
| istream& |
istream& I » vector& v |
reads v componentwise from the input stream I.
|
| double |
v.xcoord() |
returns the zero-th cartesian coordinate of v.
|
| double |
v.ycoord() |
returns the first cartesian coordinate of v.
|
| double |
v.zcoord() |
returns the second cartesian coordinate of v.
|
| int |
compare_by_angle(const vector& v1, const vector& v2) |
| |
|
For a non-zero vector v let 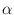 (v) be the angle by which the positive
x-axis has to be turned counter-clockwise until it aligns with v. The
function compares the angles defined by v1 and v2, respectively. The
zero-vector precedes all non-zero vectors in the angle-order. (v) be the angle by which the positive
x-axis has to be turned counter-clockwise until it aligns with v. The
function compares the angles defined by v1 and v2, respectively. The
zero-vector precedes all non-zero vectors in the angle-order.
|
| vector |
cross_product(const vector& v1, const vector& v2) |
| |
|
returns the cross product of the three-dimensional vectors v1 and v2.
|
Vectors are implemented by arrays of real numbers. All operations on a vector
v take time
O(v.dim()), except for dim and [ ] which take constant
time. The space requirement is
O(v.dim()).
Be aware that the operations on vectors and matrices incur rounding errors and
hence are not completely reliable. For example, if M is a matrix, b is a
vector, and x is computed by x = M.solve(b) it is not necessarily true that
the test b == M * x evaluates to true. The types integer_vector and integer_matrix provide exact linear algebra.









