Convex Hulls
What is a Convex Hull?A set of points On the right you see a set of points in the plane, the points on the convex hull are drawn in red. The picture is a screenshot from the example of how to compute a convex hull |
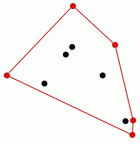 |
Example of how to compute a convex hull
The function
list<POINT> CONVEX_HULL(const list<POINT>& L)
computes the convex hull of the points in L and returns its
list of vertices. The cyclic
order of the vertices in the result corresponds to the counter-clockwise
order of the vertices on the hull. We use the notation
POINT to indicate that the algorithm works
both for points and rat_points. See also Writing
Kernel Independent Code.
Alternative Algorithms for Convex Hull
LEDA provides three different algorithms for computing the convex hull of a point set- Sweep Algorithm:
list<POINT> CONVEX_HULL_S(const list<POINT>& L);
Running time: worst and best case: O(nlogn) - Incremental Construction:
list<POINT> CONVEX_HULL_IC(const list<POINT>& L);
Running time:- worst case: O(n2)
- average case: O(nlogn)
- best case: O(n)
- Randomized Incremental Construction:
list<POINT> CONVEX_HULL_RIC(const list<POINT>& L);
Expected running time: O(nlogn)
The randomized incremental construction is the default algorithm for convex hull. It is generally faster in practice than incremental construction. It is also faster than the sweep algorithm if there are only few hull vertices. If the input points are on the unit circle the sweep algorithm is faster. More details can be found in the LEDA Book.
Convex Hulls in 3D
The function
void CONVEX_HULL(list<d3_rat_point> L, GRAPH<d3_rat_point,int>& H)
takes as argument a list
of d3_rat_points and returns the (planar embedded) surface
graph H of the convex hull of
L. The algorithm is based on an incremental space sweep.
Running Time: O(n2) in the worst case and
O(nlog n) for most inputs.
See also:
Writing Kernel Independent Code
Manual Entries
Manual Page of Geometry Algorithms
Manual Page 3D Convex Hull Algorithms