




Next: Secure Byte String (
Up: Version 6.6 The LEDA
Previous: Memory Streambuffer ( memory_streambuf
Contents
Index
Symmetric Key Cryptography
LEDA covers the following aspects of symmetric key cryptography:
- encryption (= enciphering) and decryption (= deciphering) of a
stream:
Encryption takes as input some plaintext (a stream of data) and
a key (a small piece of secret data) and outputs some ciphertext.
Decryption is the reverse operation: its input consists of the
ciphertext and a key, and its output is the original plaintext.
The idea is that the plaintext cannot be recovered from the ciphertext without
knowing the correct decryption key. This property is called secrecy.
It allows you to send the ciphertext through an insecure channel or to store
it on an insecure filesystem.
There are algorithms where the decryption key differs from the corresponding
encryption key. An algorithm which uses the same key for both operations is
called symmetric. (All algorithms provided by LEDA have this property.)
- authentication of a stream:
Authentication takes as input a message and a key and outputs a
so-called Message Authentication Code (MAC). A MAC can be seen as a
key-dependent checksum. The idea is that nobody can generate a valid MAC for a
message without knowing the key.
So if message and MAC are sent through an insecure channel then the receiver
- given that he knows the key - can verify that the text has not been
tampered with (integrity) and that it originates from someone knowing
the key (authentication). MACs are also useful if you want to make sure
that no intruder (in particular no virus) can alter a file on your system. (If
ordinary checksums were used the intruder could change the file and then
simply update corresponding checksum.)
- key generation:
The security of a cryptographic system depends heavily on the strength of its
keys. If an attacker can obtain your keys he can decrypt your messages or fake
MACs no matter how good the encryption and authentication algorithms are.
In order to support the user LEDA provides secure methods to generate a key
from a human-readable passphrase. Of course, the user has the responsibility to
chose a good passphrase, i.e. a phrase that cannot be guessed easily by an
attacker.
All these topics will be discussed in detail later.
We want to point out that secrecy and authentication are two orthogonal
concepts. If you use only authentication, nobody will be able to change your
message without being detected but everybody can read it. On the other hand,
if you use only encryption then nobody can read your message but an attacker
could change it. At first sight this does not seem to make much sense because
the attacker can only alter ciphertext and he will not be able to predict what
the corresponding plaintext will look like. However, this may still cause
damage. Imagine for example a satellite that is remote controlled via encrypted
but unauthenticated commands. If an attacker manages to make the satellite
listen to his commands, he cannot exploit the device but he might be able to
make it leave its orbit and crash.
Hence, sometimes secrecy and authentication must be used together to achieve
the desired security. LEDA makes it easy to combine these different aspects.
The example below will illustrate this.
The program is similar to the opening example of Chapter Compression. It
consists of three parts: key generation, encoding and decoding. Each part will
be explained below.
#include <LEDA/coding/crypt.h> // contains all cryptography classes
using namespace leda;
void generate_keys(CryptKey& auth_key, CryptKey& cipher_key)
{
// key generation (two keys)
CryptByteString passphrase = CryptKey::read_passphrase("Passphrase: ");
CryptByteString salt(1);
salt[0] = 'a'; // for authentication
auth_key = CryptKey::generate_key(128/8, passphrase, salt);
salt[0] = 'c'; // for enciphering/deciphering
cipher_key = CryptKey::generate_key(128/8, passphrase, salt);
}
int main()
{
string str = "Hello World";
CryptKey auth_key, cipher_key;
// encode: MAC -> compress -> encipher
typedef CoderPipe3< OMACCoder<>, PPMIICoder, CBCCoder<> > CryptCoder;
encoding_ofstream<CryptCoder> out("foo");
generate_keys(auth_key, cipher_key);
out.get_coder()->get_coder1()->set_key(auth_key);
out.get_coder()->get_coder3()->set_key(cipher_key);
out << str << "\n";
out.close();
if (out.fail()) std::cout << "error writing foo" << "\n";
// decode: decipher -> decompress -> MAC
decoding_ifstream<CryptCoder> in("foo");
generate_keys(auth_key, cipher_key);
in.get_coder()->get_coder1()->set_key(auth_key);
in.get_coder()->get_coder3()->set_key(cipher_key);
str.read_line(in);
in.finish(); // read till EOF is reached and then close "in"
if (in.fail()) std::cout << "error authenticating foo" << "\n";
std::cout << "decoded string: " << str << "\n";
return 0;
}
In the first part of the program (function
generate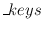 ) two keys
are generated. The input for each generation is a passphrase and a salt. The
passphrase is a human-readable and easy-to-remember string which must be kept
secret. The salt is an array of bytes (in the example just one byte) which
should be unique but it can be made public without endangering security. It
allows to generate different keys from a single passphrase. In the example we
generate one key for authentication and one key for encryption.
More information on key generation can be found in Section CryptKey.
) two keys
are generated. The input for each generation is a passphrase and a salt. The
passphrase is a human-readable and easy-to-remember string which must be kept
secret. The salt is an array of bytes (in the example just one byte) which
should be unique but it can be made public without endangering security. It
allows to generate different keys from a single passphrase. In the example we
generate one key for authentication and one key for encryption.
More information on key generation can be found in Section CryptKey.
In the second part (beginning of
main) we encode a message. We use
a coder pipe
CryptCoder which first authenticates
(
OMACCoder), then compresses (
PPMIICoder) and finally
encrypts (
CBCCoder) its source stream.
Observe that the output of the
OMACCoder (in encoding mode) is the
original input plus the MAC for this input. (In decoding mode this MAC will be
verified automatically.)
In order to use the
CryptCoder we construct an
encoding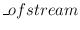 called
out. After setting the keys of
the cryptographic coders we can use
out just like an ordinary
ofstream.
called
out. After setting the keys of
the cryptographic coders we can use
out just like an ordinary
ofstream.
We want to point out that the order of the coders in the pipe is not
arbitrary. It makes sense to put the authentication at the very beginning
because you want to authenticate the original plaintext and not some compressed
or encrypted version of it. Moreover, it is important to place compression
before encryption for two reasons: Since compression usually destroys
patterns and structures in the plaintext it can be seen as a way of obscuring
the plaintext, which can be a helpful preprocessing step for encryption.
But the following is even more important: As encryption transforms its input
into a seemingly random stream applying compression after encryption usually
increases the length of stream. (Some cryptographers even warn not to trust an
encryption algorithm if its output can be compressed well [80].)
Now we describe the decoding process (at the end of
main).
It looks very similar to the encoding process but instead of
encoding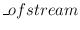 we use its counterpart
decoding
we use its counterpart
decoding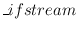 . After the key set up the stream
in
can be used as a usual C++ input stream. However, there is one subtle point
that we want to highlight: When we are done with
in we do not call
the
close but the
finish method. This reads the stream
till its end before closing it. This ensures that the
OMACCoder
verifies the MAC and reports an error if the computed MAC and the MAC found in
the stream differ.
(If
in were closed before its end is reached then no authentication
would be performed and no error would be signaled. The reader is invited to
try this out.)
. After the key set up the stream
in
can be used as a usual C++ input stream. However, there is one subtle point
that we want to highlight: When we are done with
in we do not call
the
close but the
finish method. This reads the stream
till its end before closing it. This ensures that the
OMACCoder
verifies the MAC and reports an error if the computed MAC and the MAC found in
the stream differ.
(If
in were closed before its end is reached then no authentication
would be performed and no error would be signaled. The reader is invited to
try this out.)
We want to discuss a feature of LEDA that can simplify the decoding process.
Suppose a friend of yours has sent you an authenticated and encrypted file over
the internet, and he has provided you the authentication and the encryption key
(via a secure channel). But unfortunately he did not tell you which coders he
actually used for encoding his message.
Then you can use the
CryptAutoDecoder to decode his message. This
class is able to automatically reconstruct the coder (or the coder pipe) that
was used for encoding the stream:
decoding_ifstream<CryptAutoDecoder> in("foo");
in.get_coder()->add_key(auth_key);
in.get_coder()->add_key(cipher_key);
Of course, LEDA also supports encryption and decryption of files:
// encryption
CoderPipe3< OMACCoder<>, PPMIICoder, CBCCoder<> > coder;
coder.set_src_file("input.txt"); coder.set_tgt_file("output");
coder.get_coder1()->set_key(auth_key);
coder.get_coder3()->set_key(cipher_key);
coder.encode();
// decryption
CryptAutoDecoder auto("output", "input.txt");
auto->add_key(auth_key); auto->add_key(cipher_key);
auto.decode();
We want to discuss some security assumptions made by LEDA, i.e. some
preconditions that must be fullfilled in order to ensure the security of your
data:
- Your passphrases and your keys must be safe.
That means that the user is responsible for chosing passphrases that cannot be
guessed easily by an attacker. One way to ``generate'' such a passphrase is to
take a sentence and to deliberately add some typos like ``LEDA's crytografic
algorhythms are very good!''. (If you get tired of such long phrases you could
use a phrase that consists basically of the first letter of every word:
``L'scaa++!'')
If passphrases or keys are stored on a disc this disc must be protected
against an attacker. (Also take care of temporary copies, they must be
thoroughly wiped out. Simply deleting a file does not suffice because its
contents can still be recovered with certain tools. Some specialists are even
capable of recovering data on a hard disc that has been overwritten once.)
- The main memory of your computer must be safe.
While cryptographic operations are performed passphrases and keys are stored
in plaintext in the main memory of the computer.
Therefore the user must make sure that no attacker can inspect any memory used
by his process (in particular while the process is running).
Some features of LEDA support the user in making this kind of attack harder:
The class
CryptByteString and the derived class
CryptKey
overwrite their memory before they free it and return it to the system.
We want to point out that this precaution can be foiled by the operating
system. If it swaps some security sensitive part of the memory to a swap file
on a hard disc then this data may remain there after the termination of your
process.
(On some platforms LEDA prevents this swapping, see Section CryptKey.)
We want to address another important issue. Some readers might be worried about
the fact that a potential attacker can purchase a copy of the source code of
LEDA. One may wonder if this is a security risk. Fortunately, this is not the
case.
The cryptographic algorithms in LEDA have been designed under the assumption
that a potential attacker knows the algorithm (but not the key).
All the algorithms have appeared in scientific publications and successfully
passed thorough cryptographic analysis.
The fact that the source code can be purchased allows you to verify that the
developers of LEDA did not put any trap-doors into the code which allow
them to decrypt data without knowing the key.
(This means: If you loose your passphrase or your key then we are not
able to help you to recover your encrypted data.)
Subsections





Next: Secure Byte String (
Up: Version 6.6 The LEDA
Previous: Memory Streambuffer ( memory_streambuf
Contents
Index




