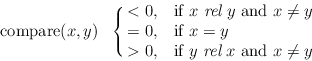





If a user defined class type T shall be used as actual type parameter in a container class, it has to provide the following operations:
| a) a constructor taking no arguments | T : : T() |
| b) a copy constructor | T : : T(constT&) |
| c) an assignment operator | T& T : : operator = (constT&) |
| d) an input operator | istream& operator > > (istream&, T&) |
| e) an output operator | ostream& operator < < (ostream&, const T&) |
| and if required by the parameterized data type | |
| f) a compare function | int compare(const T&, const T&) |
| g) a hash function | int Hash(const T&) |
Notice: Starting with version 4.4 of LEDA, the operations
"compare" and "Hash" for a user defined type need to be defined
inside the "namespace leda"!
In the following two subsections we explain the background of the required
compare and hash function. Section Implementation Parameters concerns a very
special parameter type, namely implementation parameters.
Many data types, such as dictionaries, priority queues, and sorted sequences require linearly ordered parameter types. Whenever a type T is used in such a situation, e.g. in dictionary<T,...> the function
int compare(const T&, const T&)
must be declared and must define a linear order on the data type T.
A binary relation rel on a set T is called a linear order on T if for all x,y,z in T:
1) x rel x
A function int compare(const T&, const T&)
defines the linear order rel on T if
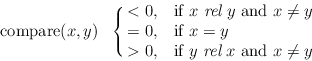
For each of the data types char, short, int, long, float, double, integer, rational,
bigfloat, real, string, and point a function
compare is predefined and defines the so-called default ordering
on that type. The default ordering is the usual ![]() - order for
the built-in numerical types, the lexicographic ordering for
string, and for point the lexicographic ordering of the
cartesian coordinates. For all other types T there is no default
ordering, and the user has to provide a compare function whenever
a linear order on T is required.
- order for
the built-in numerical types, the lexicographic ordering for
string, and for point the lexicographic ordering of the
cartesian coordinates. For all other types T there is no default
ordering, and the user has to provide a compare function whenever
a linear order on T is required.
Example: Suppose pairs of double numbers shall be used as keys in a dictionary with the lexicographic order of their components. First we declare class pair as the type of pairs of double numbers, then we define the I/O operations operator> > and operator< < and the lexicographic order on pair by writing an appropriate compare function.
class pair {
double x;
double y;
public:
pair() { x = y = 0; }
pair(const pair& p) { x = p.x; y = p.y; }
pair& operator=(const pair& p)
{
if(this != &p)
{ x = p.x; y = p.y; }
return *this;
}
double get_x() {return x;}
double get_y() {return y;}
friend istream& operator>> (istream& is, pair& p)
{ is >> p.x >> p.y; return is; }
friend ostream& operator<< (ostream& os, const pair& p)
{ os << p.x << " " << p.y; return os; }
};
namespace leda {
int compare(const pair& p, const pair& q)
{
if (p.get_x() < q.get_x()) return -1;
if (p.get_x() > q.get_x()) return 1;
if (p.get_y() < q.get_y()) return -1;
if (p.get_y() > q.get_y()) return 1;
return 0;
}
};
Now we can use dictionaries with key type pair, e.g.,
dictionary<pair,int> D;
Sometimes, a user may need additional linear orders on a data type T which are different from the order defined by compare. In the following example a user wants to order points in the plane by the lexicographic ordering of their cartesian coordinates and by their polar coordinates. The former ordering is the default ordering for points. The user can introduce an alternative ordering on the data type point (cf. Section Basic Data Types for Two-Dimensional Geometry) by defining an appropriate compare function (in namespace leda)
int pol_cmp(const point& x, const point& y)
{ /* lexicographic ordering on polar coordinates */ }
Now she has several possibilities:
DEFINE_LINEAR_ORDER(point, pol_cmp, pol_point)After this call pol_point is a new data type which is equivalent to the data type point, with the only exception that if pol_point is used as an actual parameter e.g. in dictionary<pol_point,...>, the resulting data type is based on the linear order defined by pol_cmp. Now, dictionaries based on either ordering can be used.
dictionary<point,int> D0; // default ordering dictionary<pol_point,int> D1; // polar ordering
In general the macro call
DEFINE_LINEAR_ORDER(T, cmp, T1)introduces a new type T1 equivalent to type T with the linear order defined by the compare function cmp.
dictionary<point,int> D0; // default ordering dictionary<point,int> D1(pol_cmp); // polar orderingThis alternative handles the cases where two or more different orderings are needed more elegantly.
This variant is helpful when the compare function depends on a global parameter. We give an example. More examples can be found in several sections of the LEDA book [64]. Assume that we want to compare edges of a graph GRAPH < point, int > (in this type every node has an associated point in the plane; the point associated with a node v is accessed as G[v]) according to the distance of their endpoints. We write
using namespace leda;
class cmp_edges_by_length: public leda_cmp_base<edge> {
const GRAPH<point,int>& G;
public:
cmp_edges_by_length(const GRAPH<point,int>& g): G(g){}
int operator()(const edge& e, const edge& f) const
{ point pe = G[G.source(e)]; point qe = G[G.target(e)];
point pf = G[G.source(f)]; point qf = G[G.target(f)];
return compare(pe.sqr_dist(qe),pf.sqr_dist(qf));
}
};
int main(){
GRAPH<point,int> G;
cmp_edges_by_length cmp(G);
list<edge> E = G.all_edges();
E.sort(cmp);
return 0;
}
The class
cmp
LEDA also contains parameterized data types requiring a hash function and an equality test (operator==) for the actual type parameters. Examples are dictionaries implemented by hashing with chaining ( dictionary<K,I,ch_hashing> ) or hashing arrays ( h_array<I,E> ). Whenever a type T is used in such a context, e.g., in h_array<T,...> there must be defined
Hash maps the elements of type T to integers. It is not required that Hash is a perfect hash function, i.e., it has not to be injective. However, the performance of the underlying implementations very strongly depends on the ability of the function to keep different elements of T apart by assigning them different integers. Typically, a search operation in a hashing implementation takes time linear in the maximal size of any subset whose elements are assigned the same hash value. For each of the simple numerical data types char, short, int, long there is a predefined Hash function: the identity function.
We demonstrate the use of Hash and a data type based on hashing by extending the example from the previous section. Suppose we want to associate information with values of the pair class by using a hashing array h_array<pair,int> A. We first define a hash function that assigns each pair (x, y) the integral part of the first component x
namespace leda {
int Hash(const pair& p) { return int(p.get_x()); }
};
and then we can use a hashing array with index type pair
h_array<pair, int> A;




