| int |
L.length() |
returns the length of L.
|
| int |
L.size() |
returns L.length().
|
| bool |
L.empty() |
returns true if L is empty, false otherwise.
|
| list_item |
L.first() |
returns the first item of L (nil if L is empty).
|
| list_item |
L.last() |
returns the last item of L. (nil if L is empty)
|
| list_item |
L.get_item(int i) |
returns the item at position i (the first position is 0).
Precondition
0 < = i < L.length(). Note that this takes
time linear in i.
|
| list_item |
L.succ(list_item it) |
returns the successor item of item it, nil if
it = L.last().
Precondition it is an item in L.
|
| list_item |
L.pred(list_item it) |
returns the predecessor item of item it, nil if
it = L.first().
Precondition it is an item in L.
|
| list_item |
L.cyclic_succ(list_item it) |
| |
|
returns the cyclic successor of item it, i.e.,
L.first() if it = L.last(), L.succ(it) otherwise.
|
| list_item |
L.cyclic_pred(list_item it) |
| |
|
returns the cyclic predecessor of item it, i.e,
L.last() if it = L.first(), L.pred(it) otherwise.
|
| const E& |
L.contents(list_item it) |
returns the contents L[it] of item it.
Precondition it is an item in L.
|
| const E& |
L.inf(list_item it) |
returns L.contents(it).
|
| const E& |
L.front() |
returns the first element of L, i.e. the contents
of L.first().
Precondition L is not empty.
|
| const E& |
L.head() |
same as L.front().
|
| const E& |
L.back() |
returns the last element of L, i.e. the contents
of L.last().
Precondition L is not empty.
|
| const E& |
L.tail() |
same as L.back().
|
| int |
L.rank(const E& x) |
returns the rank of x in L, i.e. its first
position in L as an integer from [1...| L|]
(0 if x is not in L). Note that this takes
time linear in rank(x). Precondition operator== has to be
defined for type E.
|
| list_item |
L.push(const E& x) |
adds a new item < x > at the front of L and
returns it (L.insert(x,L.first(),leda::before)).
|
| list_item |
L.push_front(const E& x) |
same as L.push(x).
|
| list_item |
L.append(const E& x) |
appends a new item < x > to L and returns
it (L.insert(x,L.last(),leda::behind)).
|
| list_item |
L.push_back(const E& x) |
same as L.append(x).
|
| list_item |
L.insert(const E& x, list_item pos, int dir=leda::behind) |
| |
|
inserts a new item < x > behind (if dir=leda::behind)
or in front of (if dir=leda::before) item pos into L and
returns it (here leda::behind and leda::before
are predefined constants).
Precondition it is an item in L.
|
| E |
L.pop() |
deletes the first item from L and returns its contents.
Precondition L is not empty.
|
| E |
L.pop_front() |
same as L.pop().
|
| E |
L.pop_back() |
deletes the last item from L and returns its contents.
Precondition L is not empty.
|
| E |
L.Pop() |
same as L.pop_back().
|
| E |
L.del_item(list_item it) |
deletes the item it from L and returns its contents L[it].
Precondition it is an item in L.
|
| E |
L.del(list_item it) |
same as L.del_item(it).
|
| void |
L.erase(list_item it) |
deletes the item it from L.
Precondition it is an item in L.
|
| void |
L.remove(const E& x) |
removes all items with contents x from L.
Precondition operator== has to be defined for type E.
|
| void |
L.move_to_front(list_item it) |
| |
|
moves it to the front end of L.
|
| void |
L.move_to_rear(list_item it) |
| |
|
moves it to the rear end of L.
|
| void |
L.move_to_back(list_item it) |
| |
|
same as L.move_to_rear(it).
|
| void |
L.assign(list_item it, const E& x) |
| |
|
makes x the contents of item it.
Precondition it is an item in L.
|
| void |
L.conc(list<E>& L1, int dir = leda::behind) |
| |
|
appends (
dir = leda : : behind or prepends
(dir = leda::before) list L1 to list L and
makes L1 the empty list.
Precondition: L! = L1
|
| void |
L.swap(list<E>& L1) |
swaps lists of items of L and L1;
|
| void |
L.split(list_item it, list<E>& L1, list<E>& L2) |
| |
|
splits L at item it into lists L1 and L2. More precisely,
if it! = nil and
L = x1,..., xk-1, it, xk+1,..., xn
then
L1 = x1,..., xk-1 and
L2 = it, xk+1,..., xn.
If it = nil then L1 is made empty and L2 a copy of L.
Finally L is made empty if it is not identical to L1 or L2.
Precondition it is an item of L or nil.
|
| void |
L.split(list_item it, list<E>& L1, list<E>& L2, int dir) |
| |
|
splits L at item it into lists L1 and L2. Item it
becomes the first item of L2 if dir==leda::before and the
last item of L1 if dir=leda::behind.
Precondition it is an item of L.
|
| void |
L.extract(list_item it1, list_item it2, list<E>& L1, bool inclusive = true) |
| |
|
extracts a sublist L1 from L. More precisely, if
L = x1,..., xp, it1,..., it2, xs,..., xn then
L1 = it1,..., it2 and
L = x1,..., xp, xs,..., xn.
(If inclusive is false then it1 and it2 remain in L.)
Precondition it1 and it2 are items of L or nil.
|
| void |
L.apply(void (*f)(E& x)) |
for all items < x > in L function f is
called with argument x (passed by reference).
|
| void |
L.reverse_items() |
reverses the sequence of items of L.
|
| void |
L.reverse_items(list_item it1, list_item it2) |
| |
|
reverses the sub-sequence
it1,..., it2 of items of L.
Precondition it1 = it2 or it1 appears before it2 in L.
|
| void |
L.reverse() |
reverses the sequence of entries of L.
|
| void |
L.reverse(list_item it1, list_item it2) |
| |
|
reverses the sequence of entries
L[it1]...L[it2].
Precondition it1 = it2 or it1 appears before it2 in L.
|
| void |
L.permute() |
randomly permutes the items of L.
|
| void |
L.permute(list_item* I) |
permutes the items of L into the same order as stored in the
array I.
|
| void |
L.clear() |
makes L the empty list.
|
| void |
L.sort(int (*cmp)(const E& , const E& )) |
| |
|
sorts the items of L using the ordering defined
by the compare function
cmp : E x E 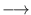 int,
with int,
with
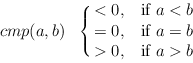
More precisely, if
(in1,..., inn) and
(out1,..., outn) denote the values of L
before and after the call of sort, then
cmp(L[outj], L[outj+1]) < = 0 for
1 < = j < n and there is a permutation
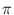 of [1..n] such that
outi = in of [1..n] such that
outi = in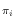 for
1 < = i < = n. for
1 < = i < = n.
|
| void |
L.sort() |
sorts the items of L using the default ordering of type E,
i.e., the linear order defined by function
int compare
(const E&, const E&). If E is a user-defined type,
you have to provide the compare function (see Section User Defined Parameter Types).
|
| void |
L.merge_sort(int (*cmp)(const E& , const E& )) |
| |
|
sorts the items of L using merge sort and the ordering
defined by cmp. The sort is stable, i.e., if x = y and
< x > is before < y > in L then < x > is before
< y > after the sort. L.merge_sort() is more efficient
than L.sort() if L contains large pre-sorted intervals.
|
| void |
L.merge_sort() |
as above, but uses the default ordering of type E. If E is a
user-defined type, you have to provide the compare function
(see Section User Defined Parameter Types).
|
| void |
L.bucket_sort(int i, int j, int (*b)(const E& )) |
| |
|
sorts the items of L using bucket sort,
where b maps every element x of L to a bucket
b(x) 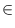 [i..j].
If
b(x) < b(y) then < x > appears before < y > after the sort.
If
b(x) = b(y), the relative order of x and y before the sort is retained,
thus the sort is stable. [i..j].
If
b(x) < b(y) then < x > appears before < y > after the sort.
If
b(x) = b(y), the relative order of x and y before the sort is retained,
thus the sort is stable.
|
| void |
L.bucket_sort(int (*b)(const E& )) |
| |
|
sorts list<E> into increasing order as prescribed by b Precondition b is an
integer-valued function on E.
|
|
() |
merges the items of L and L1 using the ordering defined by
cmp. The result is assigned to L and L1 is made empty.
Precondition L and L1 are sorted incresingly according to the
linear order defined by cmp.
|
| void |
L.merge(list<E>& L1) |
merges the items of L and L1 using the default linear order
of type E. If E is a user-defined type, you have to define the
linear order by providing the compare function
(see Section User Defined Parameter Types).
|
| void |
L.unique(int (*cmp)(const E& , const E& )) |
| |
|
removes duplicates from L.
Precondition L is sorted incresingly according to the ordering
defined by cmp.
|
| void |
L.unique() |
removes duplicates from L.
Precondition L is sorted increasingly according to the default
ordering of type E and operator== is defined for E. If E
is a user-defined type, you have to define the linear order by
providing the compare function (see Section
User Defined Parameter Types).
|
| list_item |
L.search(const E& x) |
returns the first item of L that contains x,
nil if x is not an element of L.
Precondition operator== has to be defined for type E.
|
| list_item |
L.min(const leda_cmp_base<E>& cmp) |
| |
|
returns the item with the minimal contents with respect
to the linear order defined by compare function cmp.
|
| list_item |
L.min() |
returns the item with the minimal contents with respect
to the default linear order of type E.
|
| list_item |
L.max(const leda_cmp_base<E>& cmp) |
| |
|
returns the item with the maximal contents with respect
to the linear order defined by compare function cmp.
|
| list_item |
L.max() |
returns the item with the maximal contents with respect
to the default linear order of type E.
|
| void |
L.read(istream& I) |
reads a sequence of objects of type E from the
input stream I using operator»(istream&,E&).
L is made a list of appropriate length and the
sequence is stored in L.
|
| void |
L.read(istream& I, char delim) |
| |
|
as above but stops reading as soon as the first
occurence of character delim is encountered.
|
| void |
L.read(char delim = '
\n') |
calls L.read(cin, delim) to read L from
the standard input stream cin.
|
| void |
L.read(string prompt, char delim = '
\n') |
| |
|
As above, but first writes string prompt to cout.
|
| void |
L.print(ostream& O, char space = ' ') |
| |
|
prints the contents of list L to the output
tream O using operator«(ostream&,const E&)
to print each element. The elements are separated by
character space.
|
| void |
L.print(char space = ' ') |
calls L.print(cout, space) to print L on
the standard output stream cout.
|
| void |
L.print(string header, char space = ' ') |
| |
|
As above, but first outputs string header.
|
The data type list is realized by doubly linked linear lists. Let c be the
time complexity of the compare function and let d be the time needed to
copy an object of type list<E>. All operations
take constant time except of the following operations: search, revers_items, permute
and rank take linear time O(n), item(i) takes time O(i), min, max, and unique
take time O(c*n), merge takes time
O(c*(n1 + n2)), operator=, apply,
reverse, read, and print take time O(d*n), sort and merge_sort take time
O(n*c*log n), and bucket_sort takes time
O(e*n + j - i),
where e is the time complexity of f.
n is always the current length of the list.
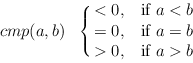
![]() of [1..n] such that
outi = in
of [1..n] such that
outi = in![]() for
1 < = i < = n.
for
1 < = i < = n.




