




Let G = (V, E) be a directed graph, let s and t be distinct
vertices in G and let
cap : E ![]() IR
IR![]() 0 be a
non-negative function on the edges of G. For an edge e, we call
cap(e) the capacity of e. An (s, t)-flow or simply
flow is a function
f : E
0 be a
non-negative function on the edges of G. For an edge e, we call
cap(e) the capacity of e. An (s, t)-flow or simply
flow is a function
f : E ![]() IR
IR![]() 0 satisfying the
capacity constraints and the flow conservation constraints:
0 satisfying the
capacity constraints and the flow conservation constraints:
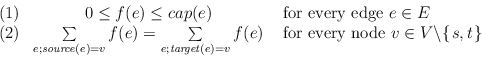
All max flow implementations are template functions. The template parameter NT can be instantiated with any number type. In order to use the template version of the function the files
#include <LEDA/graph/graph_alg.h>
#include <LEDA/graph/templates/max_flow.h>
must be included.
There are pre-instantiations for the number types int and double.
The pre-instantiated versions have the same function names except for
the suffix _T. In order to use them either
#include <LEDA/graph/max_flow.h>
or
#include <LEDA/graph/graph_alg.h>
has to be included (the latter file includes the former). The connection between template functions and pre-instantiated functions is discussed in detail in the section ``Templates for Network Algorithms'' of the LEDA book.
Special care should be taken when using the template functions with a number type NT that can incur rounding error, e.g., the type double. The section ``Algorithms on Weighted Graphs and Arithmetic Demand'' of the LEDA book contains a general discussion of this issue. The template functions are only guaranteed to perform correctly if all arithmetic performed is without rounding error. This is the case if all numerical values in the input are integers (albeit stored as a number of type NT) and if none of the intermediate results exceeds the maximal integer representable by the number type ( 253 - 1 in the case of doubles). All intermediate results are sums and differences of input values, in particular, the algorithms do not use divisions and multiplications.
The algorithms have the following arithmetic demands. Let C be the maximal absolute value of any edge capacity. If all capacities are integral then all intermediate values are bounded by d*C, where d is the out-degree of the source.
The pre-instantiations for number type double compute the maximum flow for a modified capacity function cap1, where for every edge e
The value of the maximum flow for the modified capacity function and the value of the maximum flow for the original capacity function differ by at most m*d*C*2-52.
The following functions are available:
| template <class NT> | ||
| __INLINE NT | MAX_FLOW_T(const graph& G, node s, node t, const edge_array<NT>& cap, edge_array<NT>& f) | |
| computes a maximum (s, t)-flow f in the network
(G, s, t, cap) and returns the value of the flow.
The implementation uses the preflow-push method of Goldberg and Tarjan [43] with the local and global relabeling heuristic and the gap heuristic. The highest level rule is used to select active nodes. The section on maximum flow of the LEDA book gives full information. |
||
| template <class NT> | ||
| __INLINE NT | MAX_FLOW_T(const graph& G, node s, node t, const edge_array<NT>& cap, edge_array<NT>& f, list<node>& st_cut) | |
| as above, also computes a minimum s - t cut in G. | ||
| template <class NT> | ||
| __INLINE bool | CHECK_MAX_FLOW_T(const graph& G, node s, node t, const edge_array<NT>& cap, const edge_array<NT>& f) | |
| checks whether f is a maximum flow in the network (G, s, t, cap). The functions returns false if this is not the case. | ||
| bool | MAX_FLOW_SCALE_CAPS(const graph& G, node s, edge_array<double>& cap) | |
| replaces cap[e] by cap1[e] for every edge e, where cap1[e] is as defined above. The function returns false if the scaling changed some capacity, and returns true otherwise. | ||
| template <class NT> | ||
| __INLINE NT | MAX_FLOW_T(graph& G, node s, node t, const edge_array<NT>& lcap, const edge_array<NT>& ucap, edge_array<NT>& f) | |
| computes a maximum (s, t)-flow f in the network (G, s, t, ucap) s.th. f (e) < = lcap[e] for every edge e. If a feasible flow exists, its value returned; otherwise the return value is -1. | ||
| void | max_flow_gen_rand(GRAPH<int,int>& G, node& s, node& t, int n, int m) | |
| A random graph with n nodes, m edges, and random edge capacities in [2,11] for the edges out of s and in [1,10] for all other edges. | ||
| void | max_flow_gen_CG1(GRAPH<int,int>& G, node& s, node& t, int n) | |
| A generator suggested by Cherkassky and Goldberg. | ||
| void | max_flow_gen_CG2(GRAPH<int,int>& G, node& s, node& t, int n) | |
| Another generator suggested by Cherkassky and Goldberg. | ||
| void | max_flow_gen_AMO(GRAPH<int,int>& G, node& s, node& t, int n) | |
| A generator suggested by Ahuja, Magnanti, and Orlin. | ||




