Example Delaunay Diagram
|
The following program generates a list
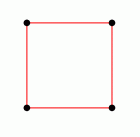
On the right you see a screenshot of the program showing the Delaunay
diagram. Clicking on the picture shows the |
 |
#include <LEDA/core/list.h>
#include <LEDA/geo/rat_point.h>
#include <LEDA/graphics/window.h>
#include <LEDA/geo/geo_alg.h>
using namespace leda;
int main()
{
list<rat_point> L;
L.append(rat_point(-75,-75));
L.append(rat_point(-75,75));
L.append(rat_point(75,-75));
L.append(rat_point(75,75));
GRAPH<rat_point,int> G;
delaunay_voronoi_kind kind;
DELAUNAY_DIAGRAM(L,G);
kind=NEAREST;
//F_DELAUNAY_DIAGRAM(L,G); //Furthest Point Delaunay Diagram
//kind=FURTHEST;
if (Is_Delaunay_Diagram(G,kind))
std::cout << "G is a Delaunay Diagram" << std::endl;
else std::cout << "WARNING: G is no Delaunay Diagram!" << std::endl;
window W;
W.init(-100,100,-100);
W.open(); W.display();
W.set_line_width(3);
rat_point p; //draw points in L
forall(p,L) {W.draw_filled_node(p.to_point(),black);}
edge e;
forall_edges(e,G) { //Delaunay Diagram
point p=G[G.source(e)].to_point();
point q=G[G.target(e)].to_point();
W.draw_edge(p,q,red);
}
W.read_mouse();
W.screenshot("delaunay_diagram");
return 0;
}
See also:
Verification of Geometric Structures