Delaunay Triangulations
A triangulation of a set S of points is a partition
of the convex hull of S into
triangles. This assumes that not all points of S are collinear.
A triangulation is called Delaunay if the interior of the circumcircle
of any triangle in the triangulation contains no points of S.
If all points of S are on the convex hull there is also
a so-called furthest site Delaunay triangulation. In a furthest
site Delaunay triangulation the circumcircle of any triangle has no points
of S in its exterior.
|
On the right you see a Delaunay triangulation of a set of points in the plane, the points and edges on the convex hull are drawn in red. The picture is a screenshot from the example of computing and verifying a Delaunay triangulation. |
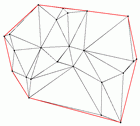 |
| On the right you see a furthest site Delaunay triangulation of a set of points in the plane, the points and edges on the convex hull are drawn in red. The picture is a screenshot from the example of computing and verifying a Delaunay triangulation. | 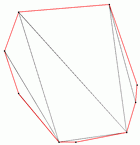 |
Properties of Delaunay Triangulations
- A Delaunay triangulation maximizes the smallest interior angle of any triangle.
- Delaunay triangulations tend to "rounder" triangles than other triangulations. This property is desirable for numerical applications.
- Delaunay triangulations are useful in many contexts.
- The Delaunay triangulation of a set of points is in general not unique.
Representation
The triangulation is represented by the parameterized graphGRAPH<POINT,int> G. G is a straight
line embedded plane map. It corresponds to the triangulation T
of the set of points L as follows:
- Nodes are in one-to-one correspondence with the points in
L Gis bidirected- For each node
vofGthe listA(v)of edges out ofvis ordered cyclically. This cyclic ordering agrees with the counter-clockwise ordering of the edges incident to the point inTcorresponding tov. - Each edge
eofGhas an integer label that gives information about the edge.G[e]=2ifeis on the convex hull ofLG[e]=0ifeis on the Delaunay Diagram ofLG[e]=1otherwise
Running Time
The running time of the algorithms is O(n2).
Verifying Delaunay Triangulations
The functionbool Is_Delaunay_Triangulation(const GRAPH<POINT,int>& G, delaunay_voronoi_kind kind)
checks whether G is a Delaunay triangulation of the points
associated with its nodes. The flag kind allows to choose
between the nearest (kind==NEAREST) and furthest (kind==FURTHEST)
site version. See also Verification of Geometric
Structures.
We use the notation POINT to indicate that the algorithm works both
for points and rat_points. See also Writing
Kernel Independent Code.
Algorithms for Constrained Delaunay Triangulations
LEDA provides additional algorithms for computing Delaunay triangulations of segments, plane maps. Details can be found on the Manual Page of Geometry Algorithms.
See also:
Verification of Geometric Structures
Writing Kernel Independent Code