Euclidean Minimum Spanning Trees

The Euclidean minimum spanning tree of a point set L is a tree of minimum cost connecting all points in L, where the cost of an edge is its Euclidean length. The Euclidean minimum spanning tree is a subgraph of the Delaunay diagram of L.

A Euclidean minimum spanning tree for a set of points L is computed as follows

1. Construct the Delaunay diagram G of L.
2. Run minimum spanning tree algorithm on G.
3. Delete all edges from G that do not belong to the minimum spanning tree.

Example

The following program generates a list L of 25 rat_points in the square (-100,-100,100,100) and computes a Euclidean minimum spanning tree for L represented by the parametrized graph G. On the right you see a screenshot of the program. Clicking on the picture shows the window in original size.

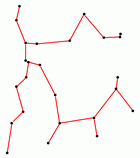#include <LEDA/core/list.h>
#include <LEDA/geo/rat_point.h>
#include <LEDA/geo/random_rat_point.h>
#include <LEDA/graphics/window.h>
#include <LEDA/geo/geo_alg.h>

using namespace leda;

int main()
{
  list<rat_point> L;
  random_points_in_square(25,100,L);

  GRAPH<rat_point,int> G;
 
  MIN_SPANNING_TREE(L,G);

  window W;
  W.init(-110,110,-110);
  W.open(); W.display();
  W.set_node_width(4);
  W.set_line_width(3);

  rat_point p;  //draw points in L
  forall(p,L) {W.draw_filled_node(p.to_point(),black);}
  W.read_mouse();
  
  edge e;
  forall_edges(e,G) { //MST
	  point p=G[G.source(e)].to_point();
	  point q=G[G.target(e)].to_point();
	  W.draw_edge(p,q,red);
  }
  W.read_mouse();

  W.screenshot("euclidean_MST");

  return 0;
}

See also:

Data Types for 2-D Geometry

Delaunay Diagrams

Minimum Spanning Trees

Windows and Panels

Linear Lists

Parametrized Graphs

Geometry Algorithms

Geometry

Graphs

GeoWin

Manual Entries

Manual Page of Geometry Algorithms