Line Segment Intersections
|
The line segment intersection problem is a basic geometric
problem. It asks to compute the set of intersections of a set On the right you see a set of 50 segments in the plane, the intesections are drawn in red. The picture is a screenshot from the example of line segment intersectionl. |
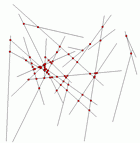 |
Example of line segment intersection
The function
void SEGMENT_INTERSECTION (const list<SEGMENT>& S,list<POINT>& P)
computes the intersections between the segments in S and returns all
proper intersections in P.
We use the notation POINT (SEGMENT) to indicate that the
algorithm works both for points (segments) and rat_points
(rat_segments) . See also Writing
Kernel Independent Code.
Remark: LEDA provides several variants for computing intersections between line segments using different algorithms and satisfying different output requirements. See the Manual Page of Geometry Algorithms and the LEDA Book for details.
Applications
- computer aided design (CAD)
- geographic information systems (GIS)
- cartography
Different applications have different output requirements, e.g., return number of intersections, trigger an action for every pair of intersecting segments, compute graph induced by segments, compute trapezoid decomposition induced by the set of segments.
Representation of Intersecting Line Segments
The set of segmentsS induces an undirected graph U(S)
as follows: Vertices of U(S) are all endpoints of segments
in S and all proper intersection points between segments in
S. Edges of U are the maximal relatively
open and connected subsets of segments in S that contain no
vertex of U(S). U(S) contains parallel edges if
S contains segments that overlap.
LEDA represents U(S) by a directed
graph G as follows.
GandUhave the same set of nodes. Each node is labeled by its position in the plane.- The edges of
Gcorrespond to the edges inU.- If the algorithm does not compute an embedding (
embed==false) there is exactly one edge inGfor each edge ofU. The edge is labeled by the segment inScontaining it and inherits the direction from the segment. - If the algorithm computes an embedding (
embed==true)Gis a planar map. For each edge ofUthere are two edges inGthat are reversals of each other. For each nodevofGthe cyclic list of edges out ofvis counter-clockwise ordered.
- If the algorithm does not compute an embedding (
See also:
Writing Kernel Independent Code