Minkowski Sums

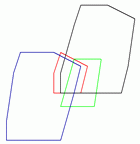
The Minkowski sum (also known as the vector sum) of two sets P and Q in R2 is the set {p+q | p in P, q in Q}. Application Areas robot motion planning computer-aided design and manufacturing (CAD/CAM) On the right there is a screenshot of the Example for Minkowski sum and difference. The polygons are shown in red and green, the Minkowski sum in black, and the Minkowski difference in blue.

Example for Minkowski sum and difference

The functions

    GEN_POLYGON MINKOWSKI_SUM(const POLYGON& P, const POLYGON& R)
    GEN_POLYGON MINKOWSKI_SUM(const GEN_POLYGON& P, const POLYGON& R)

    GEN_POLYGON MINKOWSKI_DIFF(const POLYGON& P, const POLYGON& R)	
    GEN_POLYGON MINKOWSKI_DIFF(const GEN_POLYGON& P, const POLYGON& R)

compute the Minkowski difference, i.e., the Minkowski sum of P and R.reflect(point(0,0)).

We use the notation POINT (POLYGON, GEN_POLYGON) to indicate that the algorithm works both for points (polygons , gen_polygons) and rat_points (rat_polygons , rat_gen_polygons). See also Writing Kernel Independent Code.

See also:

Data Types for 2-D Geometry

Writing Kernel Independent Code

Geometry Algorithms

Geometry

Graphs and Related Data Types

GeoWin

Number Types

Manual Entries

Manual Page of Geometry Algorithms