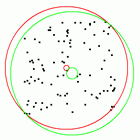
Minimum Width and Area Annuli
The functions discussed here are direct applications of Voronoi diagrams.
The function
bool MIN_AREA_ANNULUS (const list<POINT>& L, POINT& center,
POINT& ipoint, POINT& opoint, LINE& l1)
computes the minimum area annulus containing the points
of L. The function returns false if all points
in L are collinear, true otherwise. In the former case a line
passing through the points
in L is returned in l1, and in the latter case the annulus is
returned by its center and a point on the inner and the outer circle,
respectively.
The function
bool MIN_WIDTH_ANNULUS (const list<POINT>& L, POINT& center,
POINT& ipoint, POINT& opoint, LINE& l1,LINE& l2)
computes the minimum width annulus containing the points
of L. The function returns false if the minimum width annulus
is a stripe, true otherwise. In the former case the boundaries of the stripe
are returned in l1 and l2, and in the latter case the annulus
is returned by its center and a point on the inner and the outer circle, respectively.
We use the notation POINT (LINE) to indicate that the algorithm
works both for points (lines) and rat_points
(rat_line). See also Writing
Kernel Independent Code.
Running Time
Both functions have a running time O(|L|*|L|). They should only be used for small input size.Example Program for Computing Minimum Annuli
The following program computes the minimum are and minimum width annuli of a set of random points and uses a window to display the result.
#include <LEDA/core/list.h>
#include <LEDA/geo/point.h>
#include <LEDA/geo/line.h>
#include <LEDA/geo/circle.h>
#include <LEDA/geo/random_point.h>
#include <LEDA/graphics/window.h>
#include <LEDA/geo/geo_alg.h>
using namespace leda;
int main()
{
list<point> L;
random_points_in_square(100,50,L);
point acenter, aipoint, aopoint;
line al1;
bool not_collinear=MIN_AREA_ANNULUS(L,acenter,aipoint,aopoint,al1);
if (!not_collinear) cout << "All points in L are collinear!" << endl;
point wcenter, wipoint,wopoint;
line wl1,wl2;
bool not_stripe=MIN_WIDTH_ANNULUS(L,wcenter,wipoint,wopoint,wl1,wl2);
if (!not_stripe)
std::cout << "MIN_WIDTH_ANNULUS is stripe!" << std::endl;
window W;
W.init(-110,110,-110);
W.open(); W.display();
W.set_node_width(2);
W.set_line_width(2);
point p;
forall(p,L) W.draw_filled_node(p.to_point());
if (!not_collinear) W.draw_line(al1.to_line(),red);
else {
W.draw_circle(circle(acenter,aipoint),red);
W.draw_circle(circle(acenter,aopoint),red);
}
if (!not_stripe) {
W.draw_line(wl1.to_line(),green);
W.draw_line(wl2.to_line(),green);
}
else {
W.draw_circle(circle(wcenter,wipoint),green);
W.draw_circle(circle(wcenter,wopoint),green);
}
W.read_mouse();
W.screenshot("minimum_annulus");
return 0;
}
See also:
Writing Kernel Independent Code