Geometry Algorithms: Extremal Circles

Algorithmic Solutions > LEDA > LEDA Guide > Geometry Algorithms > Extremal Circles

Extremal Circles

The functions discussed here are direct applications of Voronoi diagrams.

Smallest Enclosing Circle

The smallest enclosing circle for a set L of points is the circle with the smallest radius containing all points in L. Such a circle has at least two points in L on its boundary and its center lies on the furthest site Voronoi diagram of L.
The center is either a vertex of the furthest site Voronoi diagram (three vertices of L on its boundary) or lies on an edge (two sites on the boundary).

On the right you see a smallest enclosing circle of a set of 10 points in the plane. The picture is a screenshot from the program below.

Largest Empty Circle

The largest empty circle for a set L of points is the circle with the largest radius whose interior is void of points in L and whose center lies inside the convex hull of L. Such a circle has at least two points in L on its boundary and its center lies on the nearest site Voronoi diagram of L.
The center of the circle is either a vertex (three vertices of L on its boundary) or lies on an edge of the Voronoi diagram (two sites on the boundary).

On the right you see a largest circle of a set of 10 points in the plane. The picture is a screenshot from the program below.

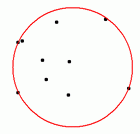
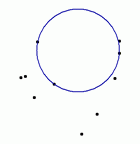
All Enclosing Circles	All Empty Circles

LEDA also provides functions to compute the list `CL` of all enclosing (picture on the left) and all empty (picture on the right) circles passing through three or more points of `L`.

Example Program for Computing Extremal Circles

The following program computes the extremal circles and was used to generate all pictures above.

#include <LEDA/core/list.h>
#include <LEDA/geo/rat_point.h>
#include <LEDA/geo/rat_circle.h>
#include <LEDA/geo/random_rat_point.h>
#include <LEDA/graphics/window.h>
#include <LEDA/geo/geo_alg.h>

using namespace leda;

int main()
{
  list<rat_point> L;
  random_points_in_square(10,50,L);  

  rat_circle C;
  //C=SMALLEST_ENCLOSING_CIRCLE(L);
  //C=LARGEST_EMPTY_CIRCLE(L);

  list<rat_circle> LC;
  ALL_ENCLOSING_CIRCLES(L,LC);
  //ALL_EMPTY_CIRCLES(L,LC);

  window W;
  W.init(-110,110,-110);
  W.open(); W.display();
  W.set_node_width(3); 
  W.set_line_width(2);
  
rat_point p;
  forall(p,L) W.draw_filled_node(p.to_point());
  //W.draw_circle(C.to_circle(),red);
  forall(C,LC) W.draw_circle(C.to_circle(),red);
  W.read_mouse();
  W.screenshot("extremal_circle");

  return 0;
}

Manual Entries

Manual Page of Geometry Algorithms

Extremal Circles

Smallest Enclosing Circle

Largest Empty Circle

All Enclosing Circles

All Empty Circles

Example Program for Computing Extremal Circles

See also:

Manual Entries